大話數(shù)據(jù)挖掘之聚類分析（上篇）
2021-01-28 14:17:45
次
人物介紹
許教授：國內(nèi)數(shù)據(jù)挖掘?qū)＜?、?85高校智能信息處理學(xué)術(shù)帶頭人
趙總：某電力公司總經(jīng)理
萬總：某超市集團營銷副總
姜局長：市衛(wèi)生局副局長
李部長：某鋼鐵集團生產(chǎn)部部長
某985高校管理學(xué)院第五屆EMBA班的《數(shù)據(jù)挖掘及其應(yīng)用》課程上。
國內(nèi)數(shù)據(jù)挖掘專家、智能信息處理學(xué)術(shù)帶頭人徐教授站在講臺上打開PPT說：“同學(xué)們，大家好！今天我們講的是數(shù)據(jù)挖掘中的聚類分析。”
“在平時的人際交往和私下的生活空間中，大多數(shù)人會自覺不自覺地加入到一個個社交圈子中。‘驢友’、‘同學(xué)會’、‘高爾夫俱樂部’，林林總總。真可謂‘物以類聚，人以群分’。”徐教授開始了聚類的講解。
“徐老師，是不是說，圈子就是聚類？”一學(xué)員問。
徐教授沒有正面回答，繼續(xù)說：“大家想一想，生活中的圈子有什么特點？”
李部長說到：“社會學(xué)家指出，‘圈子’就是由志向、趣味、地位、年齡、職業(yè)、愛好、特長、個性、收入甚至居住地點比較相近的人自發(fā)形成的團體。”
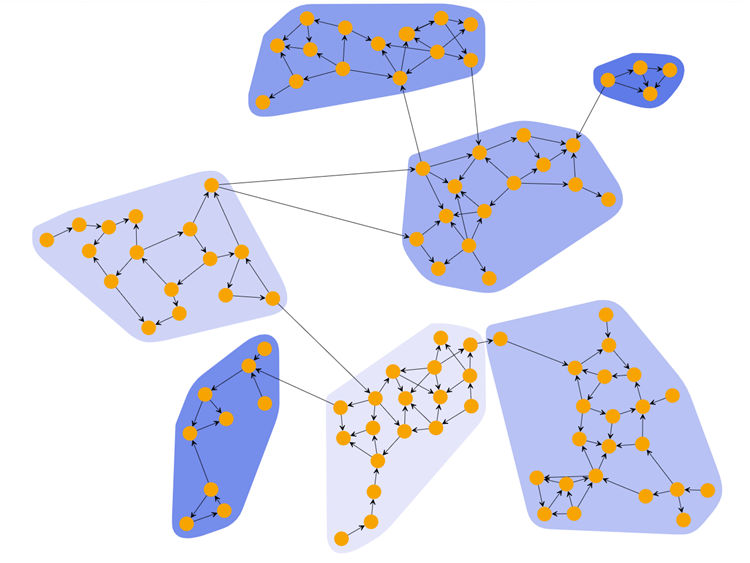
“對了，正是因為這些人具有相似的特征，他們才能聚集在一起。聚類就是將數(shù)據(jù)對象劃分成若干個類，在同一類中的對象具有較高的相似度，而不同類中的對象差異較大。”徐教授趁機給出了聚類的經(jīng)典定義。
這時，徐教授才對這位學(xué)員理解的圈子就是聚類作了正面回應(yīng)：“回答正確，加十分！”
“徐老師，從聚類的定義來看，進行聚類前并不知道所研究的對象有多少個類，聚類的過程就是通過相似性的度量，使對象聚集成若干個類，各個類的成員具有其共同的或相似的特性。”李部長說出了自己對聚類的理解。
徐教授認為李部長的理解已經(jīng)比較深刻，頻頻點頭。他因勢利導(dǎo)，又提出了一個深刻的問題：“聚類的關(guān)鍵是對象相似性的度量，大家想一想，如何度量數(shù)據(jù)對象的相似性呢？”
李部長搶答道：“兩個對象間的距離越小，說明二者越相似，用距離度量對象的相似性應(yīng)該是最自然的方法。”
徐教授滿意地點了點頭：“對，基于距離度量對象的相似性的思想，研究者提出了兩類經(jīng)典的聚類算法：劃分方法和層次聚類方法。”
趙總似乎對這兩種方法有所了解，說道：“聽我們公司數(shù)據(jù)挖掘算法組經(jīng)常說Partitioning Method和 Hierarchial Method，原來就是指的這兩類聚類算法。徐老師，昨天晚上我預(yù)習(xí)時大概了解了一下聚類算法，但理解的不夠深刻，您就給我們講講吧。”
徐教授欣然答應(yīng)，但沒有立即開始講算法，他先引導(dǎo)學(xué)員回顧基本的數(shù)學(xué)知識，問道：“大家還記得距離怎么計算？”
趙總簡潔地答道：“用歐氏距離唄！”
“對，就是大家在高等數(shù)學(xué)中經(jīng)常用到的歐幾里得(Euclid)距離。不過在聚類分析中，還經(jīng)常用到曼哈坦(Manhattan)距離、切比雪夫(Chebyshev)距離、馬哈拉諾比斯(Mahalanobis)距離等。其實，凡是滿足距離定義的四個條件即唯一性、非負性、對稱性和三角不等式的函數(shù)都可以作為距離公式。”
徐教授掃視了一下學(xué)員，覺得大家理解了距離的含義，于是說：“好了，我現(xiàn)在就簡單地介紹一下基于距離的聚類算法：劃分方法和層次方法。這兩類方法的典型代表分別為k-Means、k-Medoids和聚集、分裂算法。下面我就分別介紹這些算法。”
徐教授翻動了一下PPT，接著道：“k-Means算法的核心思想是把n個數(shù)據(jù)對象劃分為k個類，使每個類中的數(shù)據(jù)點到該類中心的距離平方和最小。”
李部長的腦子是雙核的，徐教授的話音剛落，他便道出了他的理解：“徐老師，k-Means算法本質(zhì)上是在實現(xiàn)聚類的基本思想：類內(nèi)數(shù)據(jù)點越近越好，類間點越遠越好盡可能算法。”
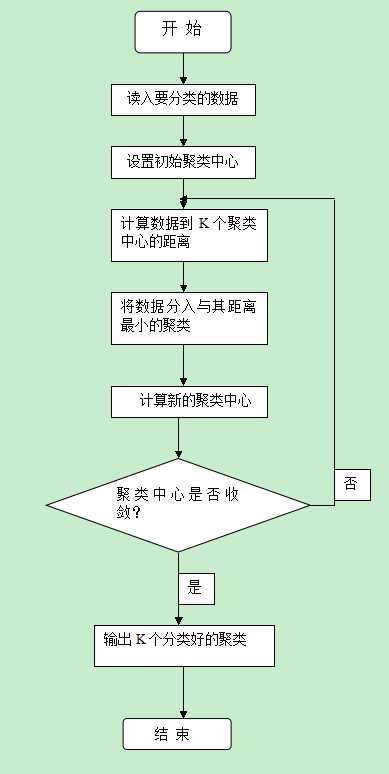
“李部長理解得完全正確，不過k-Means算法的思想只是給出了一個優(yōu)化目標(biāo)——距離之和最小，具體實現(xiàn)一般使用如PPT圖示的迭代算法。”
學(xué)員們都將注意力集中在k-Means算法框圖上，趙總看出了問題：“徐老師，k-Means算法事先就給定了聚類的個數(shù)k，然后通過迭代過程將數(shù)據(jù)點聚集到k個類中去。但是，一般情況我們并不知道數(shù)據(jù)點可以聚集成多少個類。”
“趙總說的對，k-Means算法就是要嘗試找出使平方誤差函數(shù)值最小的k個劃分，為了找出最合適的聚類個數(shù)k，一般要用若干個k去試驗，哪個k最后得到的距離平方和最小，就認為哪個k是最佳的聚類個數(shù)。”徐教授回答說。
李部長問道：“徐老師，k-Means算法第(3)步中的聚類中心是怎么計算的？”
徐教授突然冒出了個k-Medoids算法，又被李部長的雙核腦筋捕捉到了：“徐老師，k-Medoids算法只是對k-Means算法作了個小小的改變，這樣有什么作用呢？”
徐教授笑了笑，說：“k-Medoids算法用簇中最靠近中心的一個對象來代表該簇，而k-Means算法用質(zhì)心來代表簇?？梢妅-Means算法對噪聲和孤立點數(shù)據(jù)非常敏感，因為一個離群值會對質(zhì)心的計算帶來很大的影響。而k-Medoids算法通過用中心點來代替質(zhì)心，可以有效地消除這種影響。”
聽徐教授這么一解釋，李部長又大發(fā)感慨：“真是小改變，大作用??！”
趙總覺得他們電力行業(yè)對數(shù)據(jù)挖掘有迫切的應(yīng)用需求，非常關(guān)注算法的應(yīng)用效果，又問道：“k-Means算法的應(yīng)用效果怎么樣？”
徐教授：“當(dāng)結(jié)果簇是密集的，而簇與簇之間區(qū)別明顯時，k-Means算法的效果較好。對于大規(guī)模數(shù)據(jù)集，該算法是相對可擴展的，并且具有較高的效率。
李部長不僅腦子轉(zhuǎn)速高，而且善于從反面思考，他又提出了一個問題：“徐老師，k-Means算法和k-Medoids算法有哪些不足呢？”
徐教授對答如流：“首先，k-Means算法和k-Medoids算法只有在簇的數(shù)據(jù)點的平均值有定義的情況下才能使用。這可能不適用于某些應(yīng)用，例如涉及有離散屬性的數(shù)據(jù)。”
還沒有等徐教授的“其次”出口，一直只聽不說的超市集團的萬總，被徐教授的這句話觸動了，道出了她們數(shù)據(jù)挖掘時遇到的問題：“k-Means算法和k-Medoids算法一般適用于連續(xù)變量，而對于離散屬性的對象，例如兩本書，A=(小說，英文，1/32開本，浙江大學(xué)出版社)，B=(計算機圖書，中文，1/16開本，浙江大學(xué)出版社)，就無均值可言，當(dāng)然無法使用這兩種算法。那么，對于含有離散屬性數(shù)據(jù)的聚類問題怎么辦呢？”
徐教授：“為了就解決這類問題，人們對k-Means算法進行改進，出現(xiàn)了很多它們的變種，例如，k-模算法用模代替簇的平均值，用新的相異性度量方法來處理分類對象，用基于頻率的方法來修改聚類的模。而k-Means算法和k-模算法相結(jié)合，用來處理有數(shù)值類型和分類類型屬性的數(shù)據(jù)，就產(chǎn)生了k-原型算法。”
聽了徐教授的回答，萬總非常高興：”k-模算法和k-原型算法對我們可太有用了。徐老師，您就詳細給我們講講k-模算法和k-原型算法吧！”
徐教授看了看手表，說道：“今天的時間差不多了，關(guān)于k-模算法和k-原型算法的更多內(nèi)容我們下節(jié)課再講。同學(xué)們，下節(jié)課見！”
Tempo商業(yè)智能平臺
Tempo人工智能平臺
Tempo數(shù)據(jù)工廠平臺
Tempo指標(biāo)平臺
Tempo數(shù)據(jù)資產(chǎn)管理平臺
Tempo主數(shù)據(jù)管理平臺
首頁
美林?jǐn)?shù)據(jù)
大數(shù)據(jù)分析與應(yīng)用
陜公網(wǎng)安備 61019002000171號
